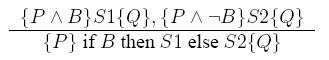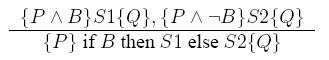| Zuweisungsaxiom: |
 |
|
| Sequenzregel: |
 |
Wenn man von P mittels S1 zu R kommt, und von R mittels S2 zu Q, so kommt man von P über die Ausführung von S1 und s2 zu Q. |
| Bedingte Anweisung: |
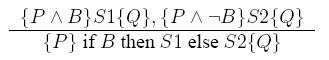 |
Wenn P und die Bedinung B erfüllt sind und man über S1 zu Q gelangt, und wenn P erfüllt ist und B nicht und man über S2 zu Q gelangt, so gilt {P} if (B) then S1 else S2 {Q}.
|
| Schleife: |
 |
Es wird eine geeignete Schleifeninvariante benötigt. Gilt diese und B ist erfüllt und ist die Invariante nach Durchlauf der Schleife unverändert und ist B nicht mehr erfüllt, ist die Schleife partiell korrekt. Für die totale Korrektheit muss noch die Termnierung bewiesen werden (siehe ALP II Skript) |